Em muitos casos podem-se ligar vários resistores num circuito elétrico que por sua vez podem ser substituídos por apenas um resistor. O resistor que substitui os vários resistores associados, sem que a corrente elétrica do circuito seja alterada, é denominado resistor equivalente.
Associação em série
A associação em série é caracterizada por ter os resistores ligados um em seguida do outro de modo que a corrente em cada um seja a mesma.
Características da associação série
1- Todos os resistores são ligados um em seguida ao outro.
2- A intensidade total da corrente elétrica i é a mesma em todos os resistores:
i = i1 = i2 = i3
3- A tensão total (U), na associação, é igual à soma das tensões em cada resistor.
U = U1 + U2 + U3
4- A resistência equivalente (Req) é igual à soma das resistências parciais.
Req = R1 + R2 + R3
De fato, se U = U1 + U2 + U3, em que U = Req . i
Assim:
U = U1 + U2 + U3
Req . i = R1 . i + R2 . i + R3 . i
como i = i1 = i2 = i3, então:
Req = R1 + R2 + R3
Exercício resolvido
Dois resistores são associados em série conforme o esquema a seguir.
Determine:
a) a resistência equivalente da associação
b) a intensidade da corrente elétrica em cada resistor;
c) a tensão elétrica em cada resistor.
Resolução
a) Como a associação dos resistores é em série, tem-se:
Req = R1 + R2
Req = 2 + 3
Req = 5 W
b) A corrente elétrica total que percorre os resistores é dada por:
U = Req . i
20 = 5 . i
i = 4 A
c) No resistor R1 tem-se:
U1 = R1 . i1
U1 = 2 . 4
U1 = 8 V
No resistor R2 tem-se:
U2 = R2 . i2
U2 = 3 . 4
U2 = 12 V
Associação em paralelo
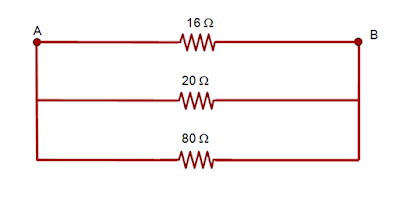
A associação em paralelo é caracterizada por ter os resistores ligados pelos seus terminais, em que, todos possuem uma extremidade ligada em A e a outra extremidade ligada em B.
Características da associação série
1- Os resistores são associados pelos seus terminais.
2- A tensão total U de toda a associação (entre A e B) é a mesma para todos os resistores:
U = U1 = U2 = U3
3- A corrente total i é a soma das correntes parciais:
i = i1 + i2 + i3
4- O inverso da resistência equivalente (Req) é igual à soma dos inversos das resistências parciais.
De fato, se i = i1 + i2 + i3, em que i = U/R
Caso particular:
Para dois resistores em paralelo:
Para n resistores iguais:
Exercícios resolvidos
1. Qual a resistência equivalente da associação a seguir?
1º. Processo:
2º. Processo
R1 com R2
2. Dois resistores são associados em série conforme o esquema a seguir.
Determine:
a) a resistência equivalente da associação;
b) a intensidade da corrente elétrica em cada resistor;
c) a intensidade da corrente elétrica total.
Resolução
a) Como a associação dos resistores é em paralelo, tem-se:
b) A tensão elétrica em cada resistor é igual à tensão elétrica total de 12 V.
No resistor R1:
U1 = R1 . i1
12 = 2 . i1
i1 = 6 A
No resistor R2 :
U2 = R2 . i2
12 = 3 . i2
i2 = 4 A
No resistor R3 :
U3 = R3 . i3
12 = 6 . i3
i3 = 2 A
c) A intensidade da corrente elétrica total é igual a soma das correntes elétricas parciais:
i = i1 + i2 + i3
i = 6 + 4 + 2
i = 12 A
Associação Mista
Quando os resistores são associados em série e em paralelo num mesmo circuito, denomina-se associação mista de resistores.
Para chegar ao resistor equivalente, deve-se resolver as associações por partes. Para isso vai-se substituindo cada associação parcial (série ou paralelo), por um único resistor reduzindo aos poucos o esquema da associação.
Exercícios resolvidos
Nos casos abaixo, calcule a resistência equivalente entre os pontos A e B.
a)
Existem casos nos quais os circuitos são mais complexos e é difícil observar as associações existentes e determinar o resistor equivalente. O melhor a fazer é refazer o circuito.
Procede-se da seguinte forma:
1º. – Marcar com uma letra diferente, cada um dos nós da associação (nó – encontro de 3 ou mais fios), lembrando que os pontos unidos por fio ideal estão em curto circuito e devem receber a mesma letra.
2º. – Refazer o circuito, iniciando pelo maior caminho encontrado desde o ponto inicial até o ponto final.
Exemplo:
1.
Marcam-se os nós e colocando letras nos mesmos:
Resolve a associação em paralelo entre A e C:
Resolve a associação em série no ramo ACB:
Resolve a associação em paralelo:
Resistor equivalente:
Curto circuito (CC)
Verifica-se que ao associar resistores em paralelo, a corrente elétrica é mais intensa no ramo de menor resistência.
Ao associar em paralelo um fio sem resistência, observa-se que toda corrente do circuito passará por este ramo enquanto que os outros resistores não serão percorridos por corrente elétrica. Neste caso, diz-se que os resistores estão em curto circuito e não funcionam.
Isto ocorre, pois com a ligação do condutor de resistência desprezível, os potenciais elétricos dos pontos A e B passam a ser iguais, então UAB = 0.
Assim, o circuito se comporta como se os resistores não existissem.
Exercícios resolvidos
1. Determine, entre os pontos P e Q, a resistência equivalente da associação.
Marcam-se os nós e colocam-se letras nos mesmos.
O ramo sinalizado, está em curto circuito pois possui as extremidades com a mesma letra. Então, pode-se cancelá-los.